이번주는 뭔가 너무 정신이 없고
바빠서 이제야 새로운 논문 리뷰를 하네요
무엇을 했냐면,
yolov7을 darknet에 구현하고 학습을 돌리느라
정신이 없었어요.
여튼 시작해봅시다
yolov7에는 repConv가 사용되었는데
그 layer를 FClayer로 바꿔준다는 논문 한번 보겠습니다.
Abstract
저자들은 RepMLP를 제안합니다. maulti layer perceptron stylen neural network building block for image recognition인데요. RepMLP는 FC layers의 series로 구성되어 있다고 하네요. convolutional layers와 비교해서, FC layers는 long-range dependencies와 positional patterns에서 더 효과적이고 더 좋은데요. 반면 local structrues을 capturring 하는데 있어서는 더 나쁘죠. 따라서 image recognition에서는 대게 덜 선호되죠. 저자들은 structural re-parameterization technique을 제안합니다. 이 technique은 local prior을 image recognition에 대해 powerful 하게 만드는 FC에 추가하는 것이라고 합니다. 구체적으로, 저자들은 training 동안 convolutional layters를 RepMLP 안에서 construct하고 inference에 대해 그들을 FC로 merge하죠. CIFAR에서 simple pure-MLP model은 CNN과 유사한 성능을 보여줍니다. traditional CNN에 RepMLP를 넣음으로써, 저자들은 ResNet의 경우 ImageNet에서 1.8% accuracy 향상, face recognition에 대해 2.9%, Cityscapes에서 mIoU 2.3%의 향상을 더 낮은 FLOPs로 달성했죠. 저자들의 intriguing finding은 global represenstational capacity와 convolution의 local prior를 가진 FC의 positional perception의 combining은 neural network의 성능 향상을 시킬 수 있다는 점입니다.
Introduction
images의 locality( i.e. pixel은 멀리 떨어진 pixel보다 가까운 pixel과 더 상관관계가 있습니다 )는 ConvNet이 image recognition을 성공적으로 만들었죠. conv layer는 오직 local neighborhood를 처리하기 때문이죠. 이 논문에서는 저자들은 이 inductive bias를 local prior라고 부른답니다.
위에서, 저자들은 long-range dependencies를 capture하는 ability에 대해 언급했었죠. 저자들은 이 논문에서 global capacity라고 부르겠답니다. traditional ConvNets는 long-ragne dependecies를 conv layers의 deep stack에 의해 형성된 large receptive fields로 모델링했는데요. 그러나, local operations를 repeating 하는 것은 계산적으로 비효율적이고 optimization difficulties를 발생시킬 수 있습니다. 이전 연구는 global capcity를 self-attention-based modules로 강화했는데요. 이들은 local prior이 없죠. ViT은 pure-Transformer model 이죠. local prior이 없기 때문에, ViT은 엄청난 양의 training data가 필요하죠 ( 약 3억장.. 이거 가능한 숫잔지 모르겠네요 )
반면에, 몇몇 images는 intrinsic positional prior을 가지고 있죠. conv layer에 의해 유용하게 사용되고요. different positions 중에 parameters를 share하기 때문이죠. 예를 들면, 누군가 핸드폰의 보안을 풀기위해 얼굴 인식을 시도할 때, 얼굴의 사진이 가운데 있어야하죠. 눈이 위에 위치하고, 코가 중간에 위치해서 그것을 할당해야하니까요. 저자들은 이런 positional prior를 사용하는 ability를 positional perception이라고 칭한답니다.
이 논문은 global capacity와 positinoal perception을 가진 ConvNet을 제공하는 FC layers 재조명하는데요. 저자들은 FC를 몇몇 case에서 conv를 대체하는 feature maps 간의 transformation으로 사용합니다. feature map을 flattening 함으로써, ( FC를 통해 feature maps를 feeding, reshaping 함으로써 ) 저자들은 positional perception을 활용할 수 있죠. 왜냐하면 이 처리를 거친 친구들의 parameters가 position-related 되어 있기 때문이죠. 그리고 global capacity 역시 활용할 수 있습니다. every output point는 every input point와 연관되어 있기 때문이죠.( conv feature map을 활용하니 당연한 이야기입니다 ) 이런 operation은 효과적입니다. speed와 theoretical FLOPs에서 말이죠. 이는 Table 4에 나타나 있죠.

주요 관심사가 parameters의 수가 아닌, accuracy와 throughput인 application scenarios에 대해, traditional ConvNet보다 FC-based model을 선호할 수 있죠. 무슨 말이냐면, GPU inference serves는 대게 수 십 GB의 memory가 있죠. parameters에 의해 채워지는 이 memory는 computations와 internal feature maps에 의해 소비되는 memory와 비교하면 minor하죠.
그러나 FC는 local prior 가 없죠. 왜냐하면 spatial information을 lost하기 때문이죠. 이 논문에서 저자들은 local prior를 FC에 통합할것을 제안합니다. 이 때 structural re-parameterization tequnie을 사용하죠. 구체적으로 저자들은 conv와 batch normalization (BN) layers를 FC에 parallel하게 construct합니다. training time 동안 말이죠. 그러고 나서 trained parameters를 inference를 위해 parameters와 latency가 줄어든 FC에 merge하죠. 이에 기반하여, 저자들은 RepMLP를 제안합니다. 이는 Figure 1에서 볼 수 있죠.

training-time RepMLP 는 FC, conv, BN layers를 가지고 있죠. 그러지 inferce-time block은 3개의 FC layers만으로 동등하개 변환될 수 있죠. re-parameterization strutual의 의미는 training-time model은 parameters의 set을 가지고 있고, 반면 inference-time model은 다른 set을 가지고 있다는 것이죠. 저자들은 전자로부터 transformed된 parameters를 가진 latter로 parameterized 합니다. 저자들은 각 inference 전에 parameters를 유도하지 않습니다. 대신, 한번에 paramters 변환하고 training-time model은 사용되지 않죠.
conv와 비교하면, RepMLP는 같은 수의 parameter를 가질 때 더욱 빠릅니다. 그리고 global capacity와 positional perception을 가지고 있죠. self-attention module과 비교하면, 더 단순하고, images의 locality를 사용할 수 있죠. 실험에서 보여주듯, RepMLP는 traditional ConvNets를 뛰어넘습니다.
저자들의 contribution을 요약하면 아래와 같습니다.
1. 저자들은 global capacity와 FC의 positional perception 사용을 제안합니다. image recognition을 위한 local prior를
가지고 있죠.
2. 저자들은 inference time cost 없이 parallel conv와 BN을 local prior를 위한 FC에 merge하는 simple, platform-
agnostic 하고 diffentiable algorithm을 제안합니다.
3. 저자들은 RepMLP를 제안하는데요. 이는 효과적인 building block입니다. multiple vision task에서 효과를 보여줍니다.
Related Work
Designs for Global Capacity
Non-local Network는 long-range dependecues를 self-attention mechanism을 통해 모델링하는 것이 제안되었죠. 각 query position에 대해, non-local module 은 query position과 attention map을 형성하고 all positions의 features를 attention map에 의해 defined된 weights로 weighted sum 함으로써 all positions aggregates하는 all positions 간의 pairwise relations를 계산합니다. 그리고 나서 aggregated feautres는 각 query position의 features에 더해집니다.
GCNet은 query-independent formulation에 기반한 simplified network를 생성합니다. 이 formulation은 less computation로 Non-local Network의 accuracy를 유지하죠. GC block에 input은 global attention pooling, feature transform, 그리고 feature aggregation을 통과합니다.
이 연구와 비교하면, RepMLP는 더 단순한데요. RepMLP는 self-attention을 사용하지 않고 오직 3 개의 FC layers만을 포함하기 때문이죠. RepMLP는 Non-local module과 GC block보다 훨씬 더 ResNet-50 의 성능을 향상시킵니다.
Structural Re-parameterization
이 논문에서는, structural re-parameterization은 conv와 BN layers를 training 동안 FC에 병렬적으로 constructing 하고 나서 inference 동안 parameters를 FC에 merging 하는 것을 말합니다. 다음 설명하는 이전 연구들은 structural re-parameterization으로 categorized될 수 있죠.
Asymmetric Convolution Block ( ACB ) 는 regular conv layers의 replacemet입니다. ACB는 horizontal( i.e 1 x 3 )과 vertical ( 3 x 1 ) conv를 사용하죠. 이는 square conv ( 3 x 3 )의 "skeleton"을 강화하죠. Reasonable performance improvements가 ConvNet benchmarks에서 실행됬고 보고되었죠.
RepVGG는 VGG-like architecture인데요. architecture의 body는 3 x 3 conv와 ReLU를 inference동안 사용합니다. inference-time architecture는 1 x 1 branches와 identity를 가지는 training-time architecture로 부터 변환됩니다.
RepMLP는 ACB와 더 관련이 있습니다. 왜냐하면 이 둘은 모두 neural network building blocks이기 때문이죠. 그러나 저자들의 contrbutions는 convolutions를 stronger하게 만드는 것이 아니라 MLP를 powerful 에게 만들어 주는 것이죠. regular conv를 대체해서 말이죠. 게다가 RepMLP 의 training-time에 convolutions는 ACB나 RepVGG block, futher improvements를 위한 convolution의 other forms에 의해 강화될 수 있죠.
RepMLP
training-time RepMLP는 3 가지 parts로 구성되는데요. Global Perceptron, Partition Perceptron 그리고 Local Perceptron이죠. 이는 Figure 1에서 찾아볼 수 있습니다. 이 section에서는, 저자들은 자신들의 formulation을 소개합니다. 모든 component를 설명하고 training-time RepMLP를 FC layers로 바꾸는지 보여줍니다. key는 simple, platform-agnosic 그리고 differentiable method 입니다. conv를 FC로 합치는 method죠
Formulation
이 논문에서는, feature map은 tensor M으로 표기됩니다. R^N x C x H x W에 포함되며, 여기서 N은 batch size, C는 channels의 수, H와 W는 height와 width를 각각 나타냅니다. 저자들은 F와 W를 사용하는데요 conv의 kernel은 F 그리고 FC의 kernel은 W를 나타냅니다. simplicity와 re-implementation을 쉽게 구현하기 위해, 저자들은 data format으로 PyTorch를, transformation을 공식화는 pseudo-code style로 합니다. 예를 들면 K x K conv를 통과하는 data Flow는 아래와 같이 나타납니다.

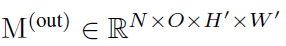
M^(out)은 output feature map이며 O는 output channels의 수입니다. p는 pad하는 pixels의 수입니다.

F는 conv kernel이며 conv는 dense를 가정합니다. ( i.e. groups의 number는 1 입니다 ). 이제부터 H' = H, W' = W를 가정합니다. 단순화를 위해서요 ( i.e. stride는 1이고 p = [k/2] 입니다. )
FC에 대해, P와 Q는 input과 output dimension이라고 하겠습니다.

V^(in)과 V^(out)은 각각 input과 output을 나타내죠.

W는 kernel입니다. matrix multiplication은(MMUL) 은 아래와 같이 공식화되죠

이제 FC에 초점을 맞춰봅시다. M^(in)을 input으로 받고 M^(out)을 output으로 뱉죠. FC는 resolution을 변화시키지 않는다고 가정합니다. ( H' = H, W' = W ) RS( reshape의 줄임말)을 사용합니다. 이는 memory에서 data의 order는 놔두고 tensor의 shape specification을 변화시키죠. 이는 cost-free합니다. input은 CHW 길이의 N vector로 flatten됩니다. 이를 수식으로 나타내면 아래와 같죠

이 V^(in)은 kernel W( OHW, CHW )에 의해 multiplied 되죠. 그러고 나서 output V^(out)이 reshaped back되죠. 그러면 M^(out)은 ( N, O, H, W ) 가 되죠. ambiguity가 없다면 저자들은 RS를 생략한다고 합니다. 즉 M^(out)을 아래와 같이 표시하겠다고 하네요

FC는 images의 locality에 이점이 없습니다. FC는 각 output point를 every input point에 따라 계산하기 때문이죠. 물론 positional imformation에 대한 인지 없이 말이죠.
Components of RepMLP
저자들은 위에 언급된 방법으로 FC를 사용하지 않는다고 합니다. 왜냐하면 local prior가 빠졌을 뿐만 아니라, 너무 많은 parameters가 존재하기 때문이죠. 그 수는 COH^2W^2 개이죠. common setting에서 ( imageNet 에서 H = W = 28, C = O = 128 ) 이 single FC는 10G parameters를 가지게 되죠. 이는 unaccpetable합니다. 이 parameters를 줄이기 위해, 저자들은 inter- and intra-partition dependencies를 각각 모델링 하는 Global Perceptron과 Parition Perceptron을 제안하죠
Global Perceptron
Global perceptron은 feature map을 splits up 합니다. different partitions가 parameters를 share할 수 있도록 하기 위함이죠. 예를 들면, ( N, C, 14, 14 ) input은 ( 4N, C, 7, 7 )로 나눠질 수 있습니다. 저자들은 모든 7 x 7 block을 partition이라 부르죠. 저자들은 memory re-arrangement의 single operation을 가지고 그런 splitting에 대해 효과적인 implementation을 사용합니다. h 와 w를 partition의 height와 width를 나타낸다고 해보죠. ( 그러니까 H, W가 h, w에 의해 나눠질 수 있다고 가정합니다, 그렇지 않다면 간단하게 input에 pad를 할 수 있겠죠 ), input M ( N, C, H, W )는 ( N, C, H/h, h, W/w, w )로 reshaped 됩니다. 이 operation은 cost-free하죠 왜냐하면 memory에서 data의 이동이 없으니까요. 그러고 나서 저자들은 axes의 order를 re-arrange합니다. ( N, H/h, W/w, C, h, w ) 이렇게 말이죠. 이는 memory에서 data가 효과적으로 move하게 해주죠. 예를 들면, 이것은 Pytorch에서 오직 permute function call 만을 요구하죠. 그런 다음 ( N, H/h, W/w, C, h, w ) tensor는 (NHW/hw, C, h, w)로 reshape되죠. 이 역시 cost-free합니다. 이는 Figure 1에서 partition map으로 보여집니다. 이런 방식으로 요구되는 parameters의 수는 COH^2W^2에서 COh^2w^2로 줄어듭니다.
그러나, splitting은 same channel의 different partitions 간의 correlations를 깹니다. 다른말로하면, 이 model은 partitions를 각각 view 할겁니다. 전체적으로 그들은 각각 positioned되었음을 인지하지 못합니다. 각각 partition에 correlations를 부여하기 위해, Global Perception은 각 partition에 대해 a pixel을 obtain하는 average pooling을 사용합니다. 그리고 BN과 two-layer MLP에 입력으로 넣어주죠. 그러고 나서 reshape하고 partition map으로 그것을 더해줍니다. 이 addition은 automatic broadcasting(i.e. ( NHW/hw, C, 1, 1 )을 ( NHW/hw, C, h, w )로 replicating )로 효과적으로 implemented 되죠. 모든 pixel이 other partitions에 관계를 맺게하기 위해서요. 그런다음 partition map은 Partition Perceptron과 Local Perceptron에 input feature map으로 입력됩니다. 이 때는 splitting이 없죠. 따라서 여기에는 Global Perceptron이 없습니다.
Partition Perceptron
Partition Perceptron은 FC와 BN layer를 가지고 있죠. partition map을 입력을 받고요. output은 ( NHW/hw, O, h, w )인데 이는 reshaped, re-arranged 그리고 inverse order로 reshaped 됩니다. 그럼 들어가기전 ( N, O, H, W )로 돌아오죠. 저자들은 FC3의 parameters를 줄이는데요. gruop wise conv에서 영감을 받았죠. group의 수로써 g를 가지고, 저자들은 groupwise conv를 아래와 같이 공식화합니다.

유사하게, groupwise FC의 knernel은 W이고 ( Q, P/g ) 에 속하죠. 여기서 g x fewer parameters를 갖죠. groupwise FC는 PyTorch와 같은 computing frameworks에서 직접적으로 지원하지 않지만, groupwise 1 x 1 conv에 의해 대체되어 구현될 수 있죠. 이 implementation은 3 단계로 구성되는데요. 1) V^(in) 을 1x1 의 spatial size를 가지는 feature map으로 reshaping합니다. 2) g group을 으로 1 x 1 conv를 수행합니다. 3) output "feature map"을 V^(out)으로 reshaping합니다. 저자들은 groupwise matrix multiplication (gMMUL)을 아래와 같이 공식화합니다.

Local Perception
Local Perception은 partition map을 input으로 받는데요. 몇 개의 conv layers를 통해 받죠. BN은 모든 conv뒤에 따라나옵니다. Fig. 1.은 h,w > 7, K = 1,3,5,7인 예제를 보여줍니다. 이론적으로, kernel size K에 대한 constraint는 K<= h, w입니다. 왜냐하면 resolution보다 큰 kenel을 쓴다는 것은 말이 되지 않죠. 그러나 저자들은 odd kernel size만을 ConvNet에 사용했습니다. K x K는 단순한 표기를 위해 사용했을 뿐이고 non-square conv ( i.e 1 x 3 or 3 x 5 ) 역시 작동하죠. conv의 padding은 resolution을 유지하기 위해 configured 되어야 합니다. ( e.g. p = 0, 1, 2, 3 for K = 1, 3, 5, 7 ) 그리고 groups g의 수는 Partition Perceptron 과 같아야 하죠. all conv branches와 Partition Perceptron의 output 은 final output으로써 더해집니다.
A Simple, Platform-agnostic, Differentiable AIgorithm for Merging Conv into FC
RepMLP를 3 개의 FC layers로 변환하기 전에, conv를 FC로 merge하는 방법을 먼저 보여주는데요. FC kernel W^(1)(Ohw, Chw), conv kernel F(O, C, K, K) ( K <= h, w ) 그리고 padding p를 가지고 W'를 construct 하길 원하는 데요. 식으로 표현하면 아래와 같습니다.

W^(1) 같은 shape의 any kernel W^(2)에 대해 MMUL의 additivity는 아래 식을 보장합니다.

따라서 저자들은 F를 W^(1)에 합칠 수 있죠. W^(1)과 같은 shape의 W^(F, p)를 manage하는 한 말이죠. 이것을 식으로 나타내면 아래와 같죠.
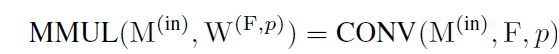
명백하게, W^(F,p)는 존재하죠. conv는 spatial positions 들 중에서 parameters를 share하는 sparse FC로써 view될 수 있기 때문이죠. translation invariance의 source 이기도 하고요. 그러나 given F 와 p 를 가진 FC를 construct 하는 것은 명확하지 않죠. modern computing platforms는 different algorithms of convoultion을 사용하기 때문에, memory allocation과 padding의 implementations가 다를 수 있습니다. specific platform에서 matrix을 constructing 한다는 의미가 다른 platform에서 작동한다라는 말은 아닙니다. 이 논문에서는, 저자들은 simple and platform-agnostic solution을 제안합니다.
위에서 언급했듯이, any input M^(in)과 conv kernel F, padding p에 대해, FC kernel W( F,p_가 존재하죠. 식으로는 아래와 같고요

위에서 다뤘던 V^(out) 식을 활용하면 아래의 식을 얻을 수 있습니다.

저자들은 identity matrix I (Chw, Chw) 를 삽입하고 associative law를 사용합니다.
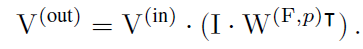
저자들은 W^(F,p) 가 F를 이용해 constructed 되기 때문에, I dot W^(F,p) 는 I 로부터 reshaped된 feature map M^(I) 에서의 F와 convolution 합니다. RS까지 표현하면 아래의 식으로 표현될 수 있죠.

이것은 명확하게 F,p 를 가진 W^(F,p)를 constructing 에 대한 expresseion이죠. 요약하면, conv kernel의 equivalently FC kernel은 proper reshaping을 가지는 identity matrix에서 convolution의 결과 입니다. conversion은 효과적이고 differentiable하죠. training 동안 FC kernel을 유도하고 objective funtion에서 사용하죠. groupwise에 대한 expression과 code는 유사한 방식으로 유도되고 supplementary material에 제공됩니다.
Converting RepMLP into Three FC layers
위의 이론을 사용하기위해, 저자들은 BN layer를 제거할 필요가 있다고 합니다. conv layers와 FC3 를 equivalently fusing함으로써 말이죠. conv kernel range와 몇몇 변수를 보죠


이 변수들은 accumulated mean, standard deviation, learned scaling factor 그리고 bais를 각각 나타냅니다. F'과 b'을 아래와 같이 정의합니다.

이렇게 정의하고 나면 아래의 식을 유도하는 것은 매우 간단해지죠

좌변은 original computation flow 입니다. 우변은 bias를 가진 constructed conv 죠. 1D BN 과 Partition Perceptron의 FC3 는 hat W와 hat b에 유사한 방식으로 합쳐질 수 있죠. 위에 W(F,p) 식을 활용하여 conv를 변환하고 resultant matrix를 hat W에 추가됩니다. conv의 bais는 hw time에 의해 간단히 대체됩니다. 왜냐하면 같은 channel에서 all points는 bias value를 공유하기 때문이죠. 그리고나서 hat b에 추가되죠. 마지막으로, 저자들은 single FC knernel과 single bias vector을 얻을 수 있었다고 합니다. inference-time FC3를 parameterize 하는데 사용되죠.
RepMLP-ResNet
RepMLP의 design 과 conv를 FC로 re-parmeterizing하는 methodology는 generic 합니다. 따라서 traditional CNNs와 all-MLP model을 포함해서 적용될 수 있죠. 이 논문에서, 저자들은 RepMLP를 ResNet에 사용했는데요. 다른 연구 전에 이미 끝났기 때문에 그 결과를 보여준다고 하네요. 그래서 MLP에 사용된 것은 다음 연구에서 보여주겠답니다.
RepMLP를 ResNet에 사용하기 위해, 저자들은 channels를 줄이는 ResNet-50의 bottleneck design principle을 따른다고 합니다. 게다가 저자들은 r x channel reduction을 RepMLP와 r x channel expansion 전에 수행했다고 합니다. whole block은 RepMLP Bottleneck으로 여겨지는데 Fig 4에 나타나있죠

구체적으로 말해보면, 저자들은 all stride-1 bottlenecks로( RepMLP Bottle을 가진 ) 대체합니다. 물론 stride-2 bottleneck은 유지하죠.
RepMLP Bottleneck의 design은 GLFP와 관련있죠. GLFP는 1x1, 3x3 conv와 FC를 가지는 bottleneck 구조죠. GLFP는 input feature maps를 vectoor로 직접 flatten합니다. 그리고나서 그들은 FC layer에 input으로 넣어주죠. 이 과정은 새롭고 insightful하지만 lagre input resolution task에서는 매우 비효율적이죠. 반면에, RepMLP는 input feature map을 나눕니다. 그리고 global information을 추가한 Global Perceptron을 사용하죠. GLFP는 3 x 3 conv branch를 local parterns를 capture 하는 1x1-FC-3x3 branch에 병렬적으로 사용하죠. Local Perceptron과 다르게 GLFP의 conv branch는 training과 inference에 필수적이죠. ( RepMLP는 inference를 위한 FC에 통합될 수 있죠 ) addition과 concatenation의 차이가 있는데요. 이 논문의 core contribution은 RepMLP를 ResNet에 insert하는게 아닙니다. conv를 FC로 re-parameterizing하는 methodology에 대해 말하는 것이죠.
여기까지 다루도록할게요.
이상 wh였습니다.



