[선형대수] Matrices and Elementary

반응형

 

Row operations

 

Linear equation을 다 쓰기는 귀찮죠. 그래서 이를 앞으로는 줄여서 표기하도록 하겠습니다. 아래처럼 말이죠

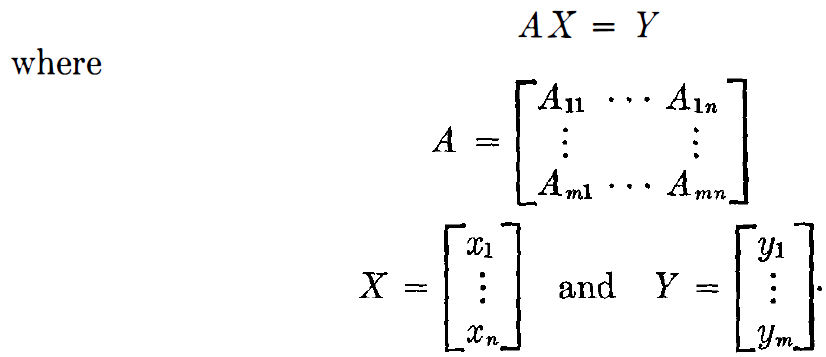
A 를 system의 matrix of coefficients 라고합니다. 분명하게 말하지만, 위에 보여진 사각 형태의 array는 행렬 이 아닙니다. 다만 , 그 형태를 빌려올 뿐이죠. field F 에 대한 m x n matrix은 ineteger ( i, j ) pairs의 set으로 부터 파생된 function A 입니다. matrix A의 entries는 A(i,j) = A_ij 이고, 이를 보기 편하게 나타나기 위해 m개의 행과, n개의 열을 가진 행렬의 형태로 나타냅니다. 이에 비슷하게, X 는 n x 1 matrix으로 Y는 m x 1 matrix으로 정의 될 수 있죠. 이 system은 간단히 AX= Y로 표현하겠습니다. 위의 matrices에 대해 multiplication을 정의 할때, Y는 A와 X의 product를 의미한다고 하겠습니다.

  이제 matrix A 의 row에 대한 opertaions를 고려해보죠. 이는 AX=Y에서 equations의 linear combinations를 form하는 것과 관련이 있죠. field F에서 m x n matrix A 에 대해 아래의 3가지 elementary row operation에 집중해봅시다.

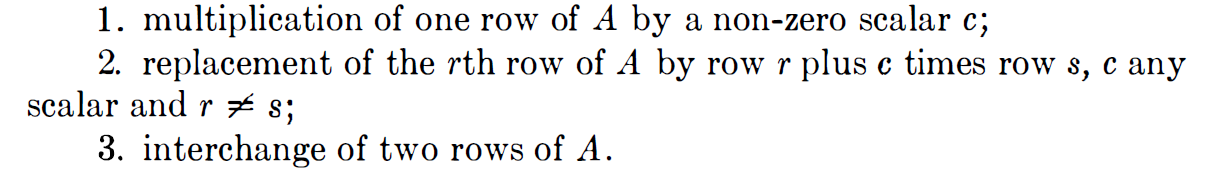
참 이게 언어로만 설명해 놓으면 무슨 말인지 알아먹기가 힘들어요. 그쵸? 위의 말을 그대로 식으로 옮기면 아래처럼 표현될 수 있습니다.

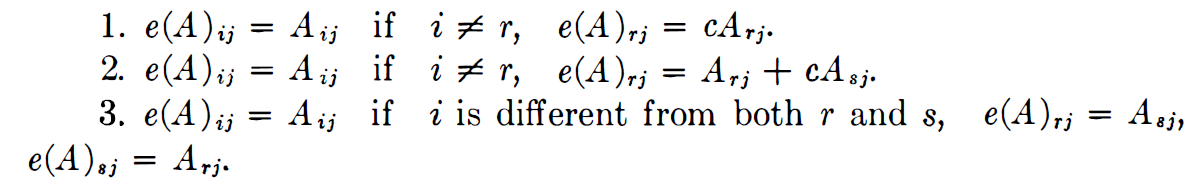
말 그대로 elementary row operation을 적용하면, if 뒤의 조건을 만족할 때 ' , '  뒤의 식을 만족한다는 소리죠. e(A)를 정의함에 있어, 얼마나 많은 columns A를 갖는 가는 중요하지 않습니다. 그러나, A의 row는 매우 중요하죠. 이것만 기억하고 갑시다. particular e 는 F에 m-rowed matrices의 class에 대해 정의됩니다. 그리고 두번 째 정리가 나옵니다.

잠깐 볼까요? 각 elementray row operaion e는 elementary row operation e1 에 해당한답니다. 즉 e_1(e(A)) = e(e_1(A)) = A 를 만족하죠. elementary row operation은 inverse operation이 존재하고, e 와 같은 타입니다. 증명에 대해 설명하지는 않겠지만 참고하실 분들은 아래의 그림을 봐주세요.

위 의 증명은 간단하게 c와 c^-1 scalar를 이용 해서 곱하고 더하고 바꾸면 같은 A를 만들 수 있음을 설명하는 겁니다. 위에 쓰여진 1,2,3,은 elementary row operation의 세 가지 type이죠. 위의 Theorm 2를 토대로 Definition이 나옵니다. 

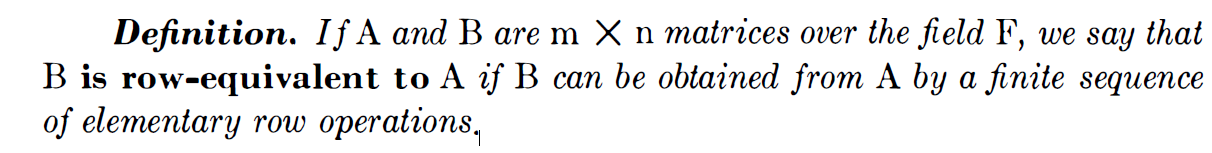
이 정의는 B 가 elementary row operations을 활용해 A로 부터 얻어 질수 있는 m x n matirx 이라면 B는 A에 row-equivalent하다는 것을 나타냅니다. 다음 나오는 Theorm 3입니다.

Theorem 3 역시, 앞에서 다룬 내용들을 이용하면 충분히 예측해 볼 수 있는 사실이죠. 위의 내용이 잘 안들어올 수 있으니 예시를 하나 봅시다.

EXAMPLE 1

F는 rational number의 field 이고 A는 아래와 같이 정의되어 있습니다.

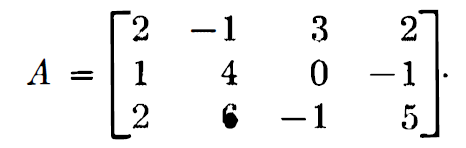
여기에 elementary row operation을 적용해보겠습니다. (2) 번을 적용하고 결과를 볼 텐데, 2번째 행에 2를 곱한 뒤 1번째 행과 빼주면 아래와 같아집니다.

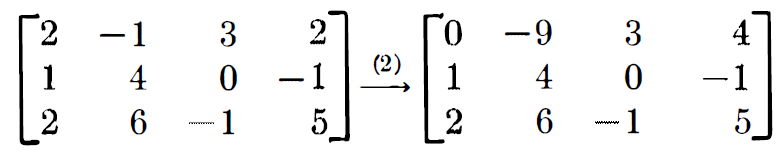
이번에는 2번쨰 행에 2를 곱한 뒤 3번째 행에 빼주겠습니다.

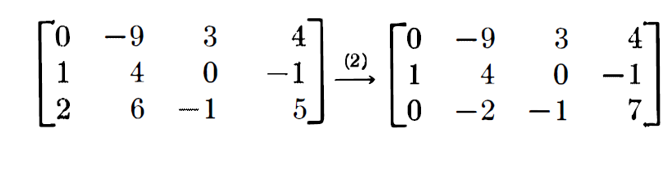
이런 과정을 반복적으로 거친다고 해보겠습니다. 물론 한 행에 특정 scalar가 곱해질 수도 있겠죠. 아래의 과정을 거쳤다고 해봅시다.

 

이 때, homogenous system이라고 하고, 변형 전 A와 변형 후 A를 활용한 system을 식으로 표현하면 아래와 같이 되겠죠.

2 번째 system과 1 번째 system은 정확히 일치하며, 2 번째 system을 통해 ( -17/3 c, 5/3, 11/3c, c )라는 solutoin을 얻을 수 있죠. 

EXAMPLE 2

이번에는 complex numbers의 field F가 있고, A가 아래와 같다고 합시다.

이번에 역시 elementar row operation을 3 행을 기준으로 적용해서 1 행과 2 행에 더해주는 과정을 거치고 1번 째 행에 대하여 ( 2-i )/3 를 곱해주는 1 번 연산을 적용하고 해당열을 이용해 정리하면 아래와 같은 과정을 얻을 수 있죠.

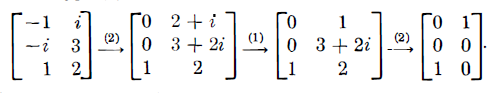
따라서 equation의 system은 아래와 같습니다.

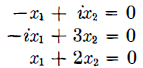
그리고 그에 대한 solution은 x_1 = x_2 = 0이죠.

 

앞의 두 개의 예제를 통해 하나의 정의가 나옵니다.

이는 unkowns를 elminating 하는 위의 두 개의 과정에서 나온 결과 matrxi을 R이라고 표현하고 row-reduced 라고 부릅니다..

EXAMPLE

row-reduced matrix의 하나의 예시는 n x n identity matrix I입니다. n x n matrix은 아래와 같이 정의되죠.

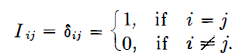
이는 Kronecker Delta를 사용해야하는 상황에 대한 many occasions 중 하나죠. ( delta 를 썼잖아요. 처음 나왔다고 이렇게 말하네요 )

  위의 앞선 두 예제에서 결과 matrices는 row-reduced matrices 였죠. 아래의 두개의 예시는 not row reduced 입니다.

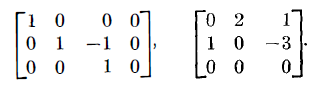
두 번째 matrix은 condition (a)를 만족하지 못하죠. 왜냐하면 first row의 non-zero entry가 1이 아니기 때문이죠. 첫 번째 matrix는 column 3에 대해 condition (b)를 만족하지 못하죠. 오늘의 모든 내용을 정리하면 하나의 Theorem 이 나오고 그는 아래와 같습니다.

오늘은 여기까지 할게요.