제 글을 꾸준히 읽어주시는 구독자 분이 계셔요
만약 어떤 부분을 올려주었으면 좋겠다고 말씀해주시면
논문이든, 뭐든 관련된 건 다 괜찮아요
더 자세히 세세히 정리해서 올려드릴게요
여튼 시작할게요
오늘은 Hungarian algorithm입니다
2022.06.30 - [AI] - SORT 구현을 위한 기초 이론 4 ( feat. Hungarian algorithm을 위한 이론들 )
SORT 구현을 위한 기초 이론 4 ( feat. Hungarian algorithm을 위한 이론들 )
안녕하세요. WH입니다. 오늘은 hungarian algorithm인데요 사실 바로 들어갈까하다가 hungarian algorithm을 위한 이론들을 쭉 정리하고 넘어가겠습니다 이번 글까지만 조금만 힘내봅시다 앞의 이론들 역시
developer-wh.tistory.com
Hungarian algorithm
헝가리안 알고리즘은 assignment problem에서 perfect matching을 위해 사용될 수 있는데요. 우선 아래의 표를 봅시다.

i 와 j 라는 각 3개의 정정에 대해 cost가 정의되어 있습니다. 예를 들면 j1과 i1을 이으면 cost 5가 발생합니다. 문제 상황은 i와 j 모두를 가장 싼 cost로 연결하는 것이 목표입니다. 그리고 그에 대한 solution이 바로 hungarain algorithm 입니다. 시작하기에 몇 가지 idea를 가지고 가봅시다. 모든 cost에 같은 값을 빼주거나 더해주면 matching이 바뀔까요? 생각해보면 cost 값이 바뀌지, matching 값은 변하지 않습니다. 그럼 질문을 바꿔보겠습니다. 행별로, 혹은 열 별로 cost를 변화시킨다면 matching이 바뀔까요? 아니요 바뀌지 않습니다. 매우 중요한 idea 입니다. 그럼 가장 싼 cost의 matching을 위해 어떤 연결들을 0으로 만들고 그 0이 겹치지 않게 선택해준다면, 우리는 원하는 solution을 찾을 수 있겠군요? 좋습니다. 계속해서 나아가 보죠. 근데 어떤 값들을 0으로 만들었는 데, perfect matching이 존재하는 지 여부는 어떻게 판단해야하죠? 이 때 konig's theorm을 사용합니다. matching의 최대 크기 = vertex cover의 최소 크기임을 이용하면 찾을 수 있겠죠. 한 가지 또 반드시 짚고 넘어가야 할 idea가 있습니다. cost는 모두 0 이상 이어야 합니다. 즉 음수 가 존재하지 않도록 합니다. 이 조건을 사용해서 귀납적인 증명을 이용하면, 원소의 합은 감소한다라는 결론을 도출할 수 있기 때문이죠. 그럼 0보다 큰데 원소의 합은 줄어들기 때문에 해당 알고리즘이 무한 루프에 빠질 위험성을 없애주게 됩니다. 따라서 이 조건 하에 알고리즘을 수행하는 것이 굉장히 중요합니다. 자자, 설명이 길었으니까 어떻게 해야하는 건지 확인해 봅시다.
Step 1 cost 변경

i1 과 모든 j에 대해 cost를 0 이상이 되도록 바꿔줍니다. 가장 작은 cost를 모든 열에 빼줍니다. 그리고 빼준 값이 얼마인지를 적어줍니다. 이를 각각 i2 와 i3에 적용해보겠습니다.

위와 같은 행렬이 나오게 됩니다. 그렇다면 이번에는 j를 기준으로 이 과정을 수행해 봅시다

그러면 cost 가 다음과 같이 바뀌겠네요?? 여기서 한번 생각을 해보는 겁니다. 모든 i와 j 쌍의 cost가 0이라면 , 우리는 가장 최소의 비용으로 matching을 완성시킬 수 있습니다. 그럼 위의 행렬은 그게 가능할까요? 여기서 konig's theorm을 사용합니다. 위의 상황을 bipartite graph로 만들면 아래와 같습니다.

konig's theorem에 따라 minmum-vetex cover = maximum matching 이죠. 위에서 vertex cover는 2임으로 perfect matching이 존재하지 않습니다. 그럼 이제 첫번째 수행으로는 perfect matching을 찾을 수 없었습니다 그럼 변형을 해봅시다. 이제 cost matrix의 0이 아닌 친구들을 고려해줄 겁니다. 0이 아닌 친구들중 가장 작은 친구를 모두 빼줍시다.
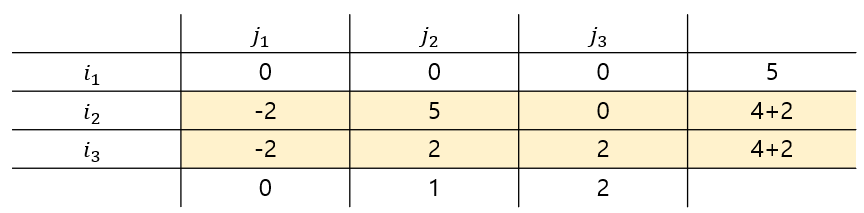
그렇게 해줬더니 -2 라는 값이 생겼습니다. 저 친구들을 없애주도록하죠 우리는 빼주는 값을 양수로 했으니 더해주는 값은 음수로 표기해 줍시다.

이제 다시 한번 perfect matching이 가능한가를 확인해봅시다. 가능하겠네요.

이렇게 말이죠. 그럼 min cost의 perfect matching을 할 수 있게 되겠네요.
이를 정리해 볼까요? 행과 열의 개수를 n이라고 해봅시다
1. 입력의 행은 i, 열은 j 각 원소는 cost로 행렬을 구성합니다.
2. 모든 행에 대해, 각 행의 가장 작은 원소의 값을 뺍니다
3. 모든 열에 대해, 각 행의 가장 작은 원소의 값을 뺍니다.
4. 행과 열을 합하여, n개보다 적게 뽑아 행렬의 모든 0의 값을 갖는 원소를 덮는 방법이 없을 때까지 loop를 돕니다.
1) 가장 크기가 작은 친구를 i', j' 라고 하고 |i'| + |j'| 이 가장 작은 것을 가져옵니다
2) 덮어지지 않은 가장 작은 값을 a 라 합시다
3) i' 에 속하지 않은 행에 대해서, 그 행의 각 원소에 a 만큼 뺍니다
4) j' 에 속하는 열에 대해서, 그 열의 각 원소에 a 만큼 더합니다
5. 행렬에서 0의 값을 갖는 원소로만 i와 j를 matching합니다.
여기까지가 hungarian algorithm에 대한 내용입니다.
SORT에서 용도
SORT에서는 matching에 사용됩니다. 즉 i와 j는 predicted와 detection object가 되죠. cost는 similarity입니다. 즉 similarity가 가장 큰 친구들에 대해 ( 1- IoU를 해주기 때문에 ) 같은 친구들이라고 matching을 해주게 되겠죠. matcing한 친구들에 ID를 부여합니다. 이것이 SORT에서의 활용도 입니다. unmatched한 친구들은 새로 생긴 object거나 remove 된 친구들이겠죠. 앞의 글들을 쭉 읽으며 용도에 대해 다시 한번 짚어보는 시간을 가지시길 바랍니다.
이상 WH였습니다.
구현은 언제할 지 모르겠습니다.
최근 갑자기 바빠져서.. 보면서 하겠습니다.
'AI' 카테고리의 다른 글
| st-gcn 코드 분석 1 (2) | 2022.10.04 |
|---|---|
| Transformer 동작 원리 이해하기 (0) | 2022.07.05 |
| SORT 구현을 위한 기초 이론 4 ( feat. Hungarian algorithm을 위한 이론들 ) (0) | 2022.06.30 |
| SORT 구현을 위한 기초 이론 3 ( feat. Kalman filter ) (0) | 2022.06.29 |
| SORT 구현을 위한 기초 이론 2 ( feat. 베이즈 필터 ) (0) | 2022.06.29 |



