SORT 구현을 위한 기초 이론 3 ( feat. Kalman filter )

안녕하세요. WH입니다.

드디어 SORT를 위한 kalman filter를 다룰 수 있게 되었습니다

베이즈 필터가 기초를 이루기 때문에 숙지하고 오시면 좋을 것 같네요

2022.06.29 - [AI] - SORT 구현을 위한 기초 이론 2 ( feat. 베이즈 필터 )

SORT 구현을 위한 기초 이론 2 ( feat. 베이즈 필터 )

Kalman filter의 용도

 kalman filter는 이전 상태만을 가지고 계산을 수행함으로 메모리 효율적이고, 연산 과정이 빠르다는 특징을 지닙니다. 대표적인 용도는 아래와 같이 정리됩니다.

 

  1. 동적 시스템 상에서 다음 수행 작업에 대해 추측을 보정합니다.

  2. 노이즈를 제거하는 데 사용됩니다.

  3. 실시간 및 임베디드 시스템 중 동적 시스템에 사용됩니다.

 Concept for kalman filter 

  먼저, 물체의 상태를 정의해 보겠습니다. 우리는 이 물체를 detection box의 center point로 잡을 겁니다. 물체의 상태를 표시하기 위해 두 가지가 필요합니다. 바로 위치와, 속도 입니다. 즉 어떤 물체의 상태는 p ( position ) , v ( velocity )로 표현해봅시다. 그럼 물체 x의 상태는 아래와 같이 표현될 수 있습니다.

  위의 식에서 문제가 하나 있는데, 그것은 바로 위치와 속도는 정확하게 특정 지을 수 없습니다. 가만 생각해보면 위치를 특정 짓는 순간 물체가 가지는 속도에 의해 물체의 위치가 변하기 때문입니다. 그래서 위치와 속도는 어떤 범위에 있을 것이라고 예측을 하는데, kalman filter에서는 이 범위에 가우시안 분포를 사용합니다. 따라서 각 변수는 평균과 분산을 가지게 되죠. 이때 분산은 uncertatinty를 의미합니다. 두 개의 변수에 관해 correlation을 따지는 것은 상당한 의미를 가집니다. 예를 들어 correlated 되었다면, ( 양의 상관 관계라고 합시다 ) 속도가 증가하면 위치가 증가하게 되겠죠. 여튼 이런 correlation을 파악하는 것 역시 kalman filter의 역할입니다. 이런 correlation은 covariance matrix를 통해 정의될 수 있습니다. 그럼 예측치 x와 x를 구성하는 v와 p 사이의 covariance marix를 표현해보겠습니다.

  위의 식은 ( k - 1 )의 상태를 가지고 k 시점의 상태를 예측한 것을 수식으로 나타낸 것입니다. 그러면 이를 잠깐 생각해보면 k-1을 통해 k 의 상태를 어떻게 변화시킬 수 있을까요? 간단한 운동 방정식을 활용해 상태 변화를 나타낼 수 있습니다.. 즉 k-1 의 위치에 t 시간 만큼 v_k-1의 속도로 움직였다고 하고 등속도 운동이라는 가정을 하면, 아래와 같이 표현할 수 있습니다.

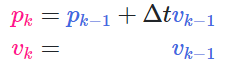
이를 x에 반영해서 prediction matrix를 만들어보면

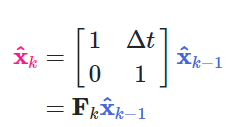
F_k 가 prediction matrix가 됩니다. 이제 우리가 알아야 할 것은 P_k가 어떻게 변화하는 지 입니다. covariance matrix 의 성질 중 아래와 같은 성질이 있습니다.

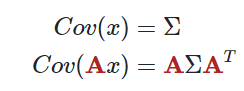
이 성질을 활용하면 P_k는 아래와 같이 표현됨을 알수 있습니다.

그런데 만약 가속도가 있어 물체의 위치를 변화 시키는 요소가 더 있다면 어떻게 될까요? 이런 문제를 다루는 행렬을 control matrix이라 합니다. 즉 position과 velocity 가 아래와 같이 표현되는 상황을 가정해봅시다.

 

이를 x로 표현하면

위와 같이 나타나게 되며, 이 때 B_k를 control matrix, u_k를 control vector라고 합니다. 계속해서 나가보겠습니다. 만약에 물체가 위와 정의한 데로 움직이다가 예기치 못한 상황을 만나면 우리는 이를 어떻게 반영해야 할까요? 이를 반영한 것이 바로 uncertainty 이고 앞서 말한 분산에 해당합니다. 그러면 우리는 이제 x를 특정 위치가 아닌 범위로 생각하면 됩니다. 왜 범위로 생각하냐, 어떤 예기치 못한 일에 따라 속도가 달라질테니까요. 즉 예측치 x_k는 예측치 x_k-1에서 바로 이동한 것이 아니라, x_k-1에서 공분산 Q_k를 가지는 어떤 분포의 범위를 가지는 영역으로 이동했다고 생각하면 됩니다. 즉 기존의 식에 이 상황을 대입하면, 아래와 같습니다.

자, 이제 이 내용을 모두 종합해 Kalman filter를 이해해보도록 하겠습니다.

estimation 과 measurement

  센서 값은 measurement 라고 생각하시면 됩니다. 그리고 prediction은 위의 concept에 의한 estimation입니다. prediction 과 estimation 사이에는 unit 이나 scale 차이가 있기에 estimation을 prediction에 맞춰주는 변환이 필요합니다. 이 때 사용하는 변환 행렬을 H_k라고 해봅시다.

그러면 예측치 x와 P ( covariance marix )는 아래와 같이 변환됩니다.

measurement 역시 완벽하게 신뢰할 수 없습니다. 그런데 위처럼 변환하게 되면 measurement의 noise를 고려하지 않는 것이 되죠. 그렇다면 이런 방법을 사용해 볼 수 있습니다. estimation을 measurement의 범위로 변환하는 방법이 있습니다. 그렇게 되면 noise를 cover할 수 있게 되죠. 그러면 우리는 두 가지 분포를 가지고 가장 합당해 보이는 분포를 만들어야 합니다. 다루어야할 분포 두 가지는 estimation이 가지는 분포와 measurement가 가지는 분포가 되겠죠. 여기서 두 분포가 overlap 된 부분이 있다면 이 부분을 가장 신뢰할 수 있는 분포임으로 overlab 된 영역이 하나의 기준이 될 수 있게죠. 해당 영영의 mean과 variance는 어떻게 구할까요? 바로 각각의 가우시안 분포의 곱을 통하여 구할 수 있습니다.

 

가우시안 분포는 아래의 식을 갖습니다.

그리고 아래 그림은 우리의 문제 상황을 그림으로 표현한 것 입니다.

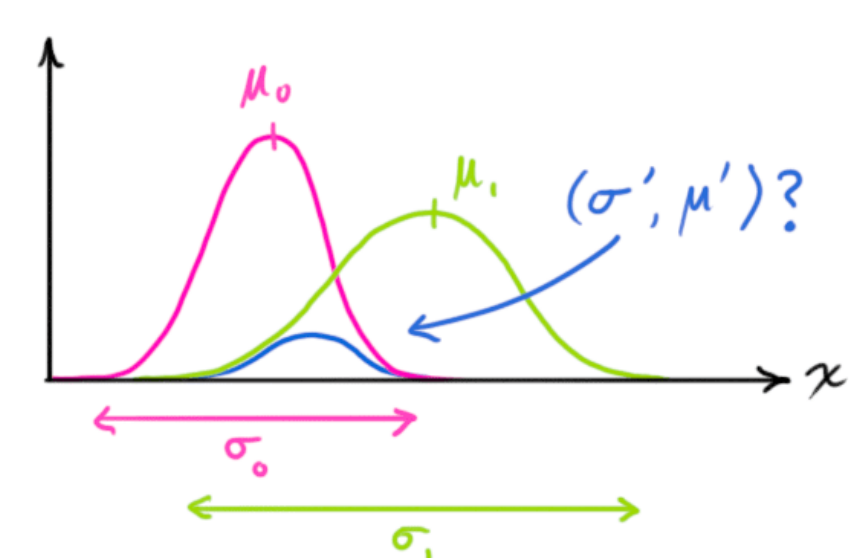
새로운 mean과 variance는 아래와 같이 계산됩니다.

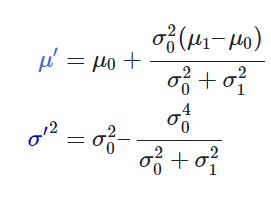
만약 k를 아래와 같이 정한다면

위 식은

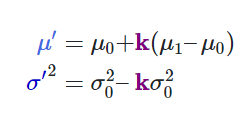
와 같이 재정의 될 수 있습니다. 이를 2차원 matrix로 확장하게 되면 

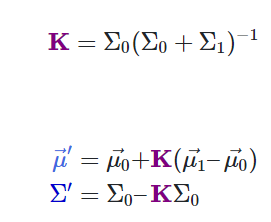
위의 식으로 확장할 수 있으며, 이 때 K matrix를 kalman gain이라고 합니다. 그러면 이 식에 위의 내용을 더하면

로 정리할 수 있으며 이 과정을 update step이라고 합니다.

SORT 에서 kalman filter의 의미

오늘 이 부분이 가장 핵심이 아닐까 합니다. 시작하겠습니다. 우선 우리가 사용하는 detector를 사용해서 매 frame마다 detection을 수행합니다. 이 때 detector에서 detected object는 measurement에 해당합니다. 그렇다면 한 가지가 더 필요합니다. 바로 estimation입니다. 그럼 이 estimation을 어떻게 구성할거냐. 이 때 이전 프레임의 detection 정보를 활용합니다. 두 frame간 시간과 위치를 활용해 운동방정식을 만들고 예측치 x 와 그에 대한 covariance matrix을 만듭니다. 이 두 가지를 활용해서 다음 frame의 detection box의 position을 예측하게 됩니다. 이 과정에는 그러면 보정 과정 역시 모두 포함이 되겠죠. 그런 다음 다음 frame이 오면 detected object와 predicted 된 친구들을 비교해서 ID를 부여함으로써 tracking이 이뤄지게 되겠죠. 그럼 한 가지 고려할 만한 대상이 있습니다. 만약 우리가 매우 제한된 상황에 있다고 가정해봅시다. 즉 computing power가 매우 떨어지는 임베디드 환경에서 tracking을 해야하는 상황이라면요? 그럼 kalman filter를 사용하지 않고 구현하면 어떻게 될까요? 아마도 속도가 매우 증가할겁니다. 그리고 frame 속도가 매우 빠르고 detector의 성능이 좋다면 kalman filter를 제외하더라도 성능 저하는 눈에 띌만큼은 아닐겁니다. ( 아닐 수도 있지만요.. ) 뭐 구현할 때 결과로 확인해봅시다.

 

이번 글에서는 kalman filter와

SORT에서 kalman filter가 어떻게 활용되는지에 대해 알아보았습니다

다음 글에서는 hungarian algorithm과

SORT에서의 활용도에 대해 알아보겠습니다.