SORT 구현을 위한 기초 이론 1 ( feat. 코드를 통한 flow 이해하기 )
안녕하세요. WH입니다.
SORT를 구현해보려고 하는데요
우선 구현하기에 앞서 필요한 이론들을 정리하는
시간을 가져보려고 합니다.
SORT ( simple online and realtime tracking )의 흐름
SORT의 흐름을 간단하게 표현해보면 이렇게 됩니다.
1. object detion
2. Kalman filter를 이용한 tracklet 형성 ( tracklet은 쉽게 다음 frame의 object 에 대한 예측이라고 생각하면 될 것 같아요 )
3. IoU tracker를 통한 similarity 계산
4. Hungarian Algorithm을 통한 matching
대략 이렇게 정리될 수 있습니다. 물론 similarity의 long term range를 cover하기 위해서는 Re-ID를 이용한 apperance를 고려해주면 되긴하지만, 복잡해지니까 그런 과정은 생략해보록하죠, Byte를 구현할 일이 있다면 여기서 발전된 형태의 모습을 보여드리도록 하겠습니다. 뭐 여튼 각설하고 다시 돌아와서 위의 flow를 따른다고 했을 때, 알아야 하는 이론에는 무엇이 있을까요?
우선 detector를 무엇을 사용하느냐에 따라 detector에 대한 이론이 필요할 겁니다. 그리고 kalman filter를 이해하기 위해서는 bayes filter 를 기본으로 함으로 bayes filter에 대한 선수 지식이 필요하지요. IoU tracker를 위해서는 IoU를 알아야 하겠고, Hungarian Algorithm을 알기 위해서는 Bipartite matching 에서 Konig's Theorem을 알아야 하지요. 이렇게 쓰고 보니.. 너무 많나요? 하나하나 다뤄보도록 하겠습니다. 우선 detector에 대한 이론은 생략하도록 할게요.
이론들을 들어가기에 앞서서 코드에서는 어떻게 구현하고 있는가를 보도록 합시다. https://github.com/mcximing/sort-cpp 의 코드를 기반으로 flow를 잡고 저것을 python으로 바꿔보도록하죠. 물론 그 과정에서 간단하게 바꿔 구현할 수도 있겠지만요.
Tracking algorithm flow
Box input -> Initailization -> Get predicted box -> Compute Similarity -> Matching -> Update -> Box output
이런 flow로 구현이 되어 있습니다. 그럼 어떻게 되는 지 코드와 함께 보도록 합시다.
Initialization

이 부분을 다루는 이유는 tracker에 대한 initalization이 프로그래밍적으로 중요하기 때문인데요 생각해보면 tracker는 예측된 친구입니다. 그런데 이 친구는 처음에는 존재할 수가 없어요. 첫 frame에서 예측이란 존재할 수 없기 때문이죠. 그래서 if 문을 통해 처리해줍니다
trackers.size() = 0 말 그대로 처음 시작이면 을 뜻합니다. 그리고 나서 KalmanTracker Class의 instance에 첫 frame에서 detector로 detect된 object의 정보를 넣어주게 됩니다. 아 과정은 다른 object가 나오면 다시 실행되는 데요. trackers는 instance이기 때문에 class 별로 ( 사람, 얼굴 등 ) 실행이 됩니다. 위에서 언급한 kalman tracker class는 c++에서의 class이고 방근 언급한 class는 detection 대상입니다. ( 헷갈리시지 않도록 색으로 구분하겠습니다 )
Get predicted box

이 과정이 kalman filter를 이용하는 부분입니다. 이론 파트에서 설명하겠지만 kalman filter의 결과물 ( Line 226 ) 은 Box information이며 predictedBoxes.push_back( Line 229 ) 를 통해 넣어주게 됩니다. 조건문의 내용은 검출된 Box information이 있다면, 추가하고 그렇지 않으면 tracker에서 지우라는 내용입니다.
Compute similarity

코드의 flow를 보면 각 frame에서 predicted box 들과 detection objects들의 IoU를 통해 Hungarian algorithm을 위한 matrix을 만듭니다. 주석 252는 중요한 정보를 던져주는데, IoU를 그대로 이용하면 안되고 Hungarina algorithm이 max matching with minimun cost assignment 이기 때문에 1 - IoU로 구현하게 됩니다. 여기서 알 수 있는 사실은 IoU가 Hungarian Algorithm을 위한 cost로 활용된다는 점은 기억하고 갈만합니다.
Matching

matching은 hungarian algorithm을 풀어사용하게 됩니다. Matching은 여기서 끝나지 않는데요. ID를 부여해야 하고 unmatched box에 대한 처리도 남아있습니다

그 처리에 대한 codeflow를 보면 detNum 이 크다면, 즉 unmatched detection이 있다면 allItems와 matchdItems 를 가지고 비교해 unmatchedDetections에 추가해주고, 만약 trkNum이 크다면, 즉 unmatched trajectory가 있다면, unmatchedTrajectoris에 넣어주게 됩니다. 또한 update 전에 low IoU를 제거하는 부분을 가지는데요. 이는 ByteTrack 이전까지 대중적으로 사용되지 않았나 합니다. ByteTrack에서는 all detection information을 모두 활용하니까요 여튼 filtering하는 부분은 아래와 같습니다

Line 296번에 1- iouMatrix 이 부분은 matrix을 구성할 때 low cost를 위해 1 - iou로 값을 계산했기 때문에, 원래 iou를 구하기 위해 1- iouMatrix을 해준 것입니다. IoU가 낮은 친구들 역시 unmatchedTrajectories와 unmatchedDetections에 넣어줍니다. 그리고 기준 IoU를 넘는다면, matchedPairs에 넣어줌으로써 ID를 부여하게 되죠
Updating
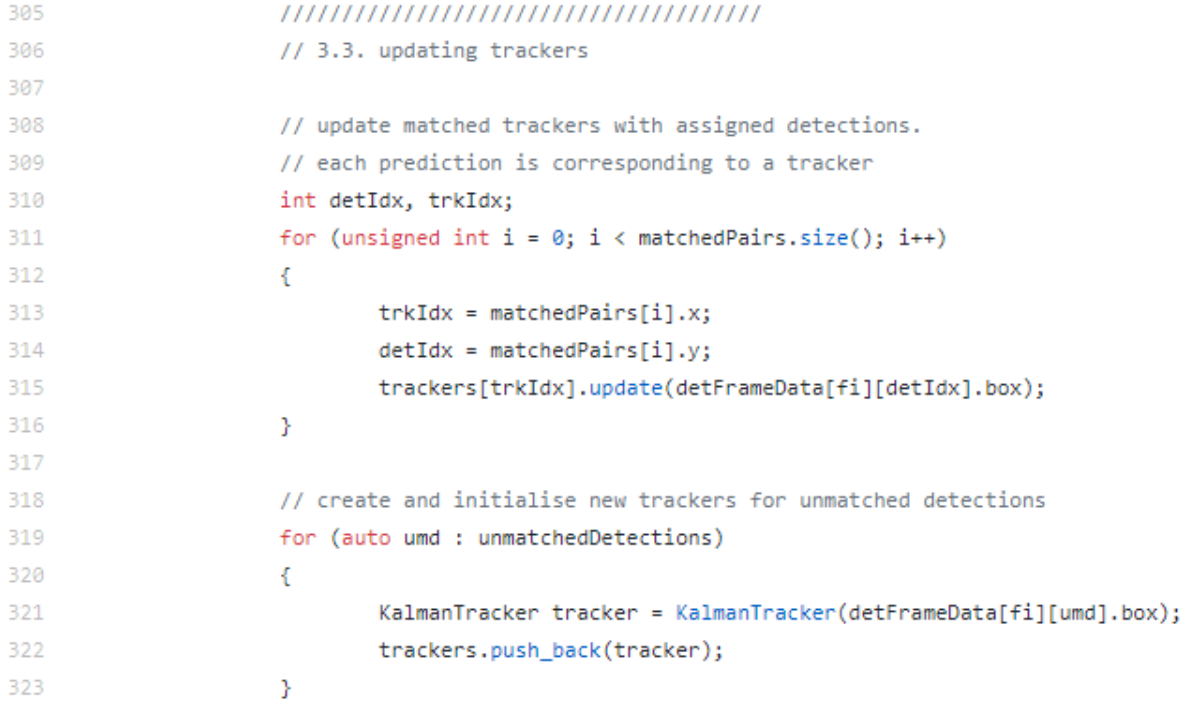
update 해주는 것은 간단합니다. assigned detectiond을 가진 matched tracker를 update 해주면 됩니다. 부여된 ID에 맞게 update해줘야 한다는 겁니다. 뿐만아니라 unmatched detection도 처리를 해주는 데요. Kalmantracker에 넣어 다시 돌려주고 새로운 tracker를 생성하고 초기화해주게 됩니다.
Output

이제 tracker를 가지고 box를 그려주기만하면 됩니다. 그리고 흥미로운 부분이자 꼭 챙기셔야할 부분은 dead tracklet에 대한 처리입니다. Line 343에서 처리합니다. 이게 matching 및 update 과정이 아닌 output 과정에서 이루어 진다는 사실을 짚고 넘어가시면 좋겠습니다.
이번 글은 여기까지인데요.
이 글의 목적은 코드 리뷰가 아닙니다.
다만 이 내용을 통해 flow를 잡고
다음 글부터 그에 맞는 기초 이론을 다져가고자 하는 겁니다.
마지막으로는 그에 대한 구현이 되겠지요
필터와 알고리즘을 구현하는 부분은 조금 생각좀 해보겠습니다.
라이브러리를 쓰면 의미가 퇴색되는 것 같고.. 고민이 많네요
여튼 제 시간을 보고 결정할게요 ㅎㅎ 이상 WH였습니다.